Posted 2019-10-24Updated 2021-11-12Leetcode4 minutes read (About 542 words)0 visits

LinkedList Cycle问题

在LinkedList中查看是否存在cycle，使用的主要方法是Floyd’s Tortoise and Hare算法，原理就是设置两个快慢指针，如果存在cycle，那么快慢指针一定会相遇。
当然不止LinkedList可以使用这个方法，只要我们能把题目类比成LinkedList(也就是前一个数能找到后一个数，其实就是LinkedList的作用)，然后题目中存在环，那么也就可以使用这个方法。

Linked List Cycle：

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while(fast!=null && fast.next!=null){
            slow = slow.next ;
            fast = fast.next.next;
            if(slow == fast){
                return true;
            }
        }
        return false;
    }
}

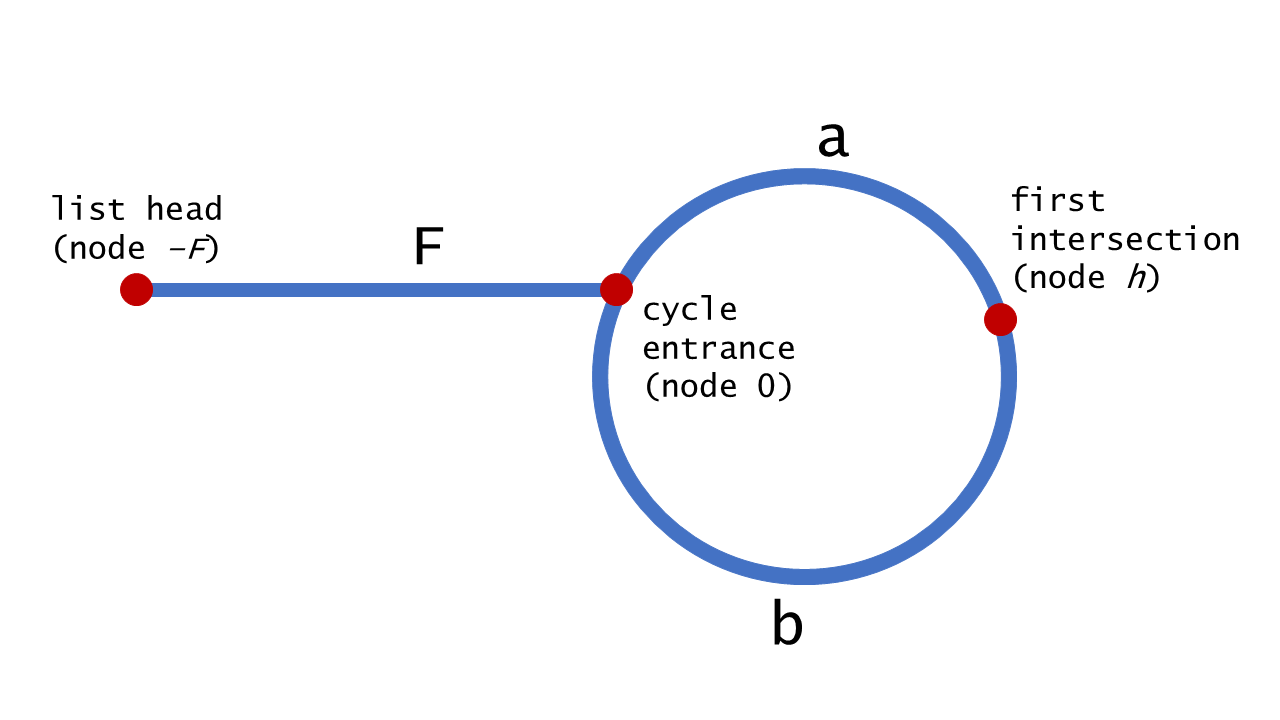
Linked List Cycle II：快慢指针相遇的时候，我们可以找到重合点，题目要求是找到cycle的起点。通过观察我们发现很重要的一个关系是快指针走了慢指针的两倍，所以从ListNode的head到cycle起点==intersect到cycle起点。

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while(fast!=null && fast.next !=null ){
            slow = slow.next;
            fast = fast.next.next;
            if(slow == fast){
                while(head!=slow){
                    head = head.next;
                    slow = slow.next;
                }
                return head;
            }
        }
        return null;
    }
}

Happy Number:
这道题不是LinkedList，但是我们发现我们总是可以从前一个数得到后一个数，并且如果最后不收敛到1的话就证明一定有环，所以可以使用Floyd’s Tortoise and Hare算法。

class Solution {
    public boolean isHappy(int n) {
        int slow = n;
        int fast = n;
        while(fast!=1){
            slow = compute(slow);
            fast = compute(compute(fast));
            if(slow==fast){
                break;
            }
        }
        
        if(fast==1){
            return true;
        }
        else {
            return false;
        }
        
    }

    private int compute(int input){
        String s = ""+input;
        int ans = 0;
        for(char c:s.toCharArray()){
            ans = ans + (c-'0')*(c-'0');
        }
        return ans;
    }
}

Find the Duplicate Number：由题目的条件可以知道所有的数在[1, nums.length-1]的范围，所以相当于我们拿到一个数，她的下一个数可以用这个数作为index找到，也就变相实现了Linkedlist，那么LinkedList的头相当于index of 0。

class Solution {
    public int findDuplicate(int[] nums) {
        int slow = nums[0];
        int fast = nums[0];
        while(true){
            slow = nums[slow];
            fast = nums[nums[fast]];
            if(slow==fast){
                break;
            }
        }
        
        slow =  nums[0];
        while(slow!=fast){
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }
}

LinkedList Cycle问题

LinkedList Cycle问题

Catalogue