Top K类型题(bucket sort, inplace quick sort and Comparator)
Top K类型题(bucket sort, inplace quick sort and Comparator)
基本类top k
今天总结了一下Top K这种类型的题目的做法,总的来说一般有三种做法:
- 最简单的就是进行sorting,然后取前K个,时间复杂度是O(nlogn)
- 第二种做法是使用Priority Queue(最小堆),Priority Queue只存储目前遇到的最大的K个元素,每次堆中元素大于K的时候我们就poll出目前最小的元素(已经有K个比他大,他肯定不是结果了),那么时间复杂度是O(nlogk)
- 最复杂的做法是使用Quick Select,由于我们只关心前K个元素,所以相当于对于Quick Sort,我们每次partition只取一半,所以时间复杂度只有O(n)。(T(n) = T(n/2) + n)
注意:当我们是求某一个频率的前K个元素的时候,我们可以不用复杂的Quick Select,而是使用简单的Bucket sort。这里能够使用bucket sort的原因在于元素的frequency肯定不大于数组的长度,也就是说有一个固定的边界。我们知道bucket sort能够使用的条件就是有固定的边界。而求取前K个最大的元素,由于元素的大小是没有边界的,所以无法使用bucket sort,我们只能用Quick Select。
这类题目通常需要使用到Comparator对元素进行比较,下面也总结一下Comparator的三种构造用法:
- 最原始的定义:Comparator是一个接口,所以我们需要声明一个类来实现这个接口,然后我们在实例化这个声明的类
1
2
3
4
5
6
7
8class myComparator<Integer> implements Comparator<Integer> {
// Compare:第一个比第二个大是1,第一个比第二个小是-1
public int compare(Integer i1, Integer i2){
return freq.get(i2) - freq.get(i1);
}
}
PriorityQueue<Integer> pq = new PriorityQueue<>(new myComparator<>()); - 简单一点的写法是使用匿名类,也就是不去手动声明一个类来实现这个接口,而是直接在这个接口后面声明一个匿名类来起到想同的效果
1
2
3
4
5
6PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>(){
public int compare(Integer i1, Integer i2){
return freq.get(i2)- freq.get(i1);
}
}); - 最简单的写法是使用java8的lambda function
1
2
3PriorityQueue<Integer> pq = new PriorityQueue<>((a, b)->{
return freq.get(b) - freq.get(a);
});
下面是几道这种类型的题。
Top K Frequent Elements: 由于是要先求频率的题,而频率是有边界的,所以最好的做法是使用bucket sort,时间复杂度O(n),空间复杂度O(n)。
Top K Frequent Words
Kth Largest Element in an Array: 由于是取最大的K个数,是没有边界的,所以用应该用quick select,时间的复杂度O(n),空间复杂度O(1)。
K Closest Points to Origin
quick select的inplace实现:
https://blog.csdn.net/qq_20011607/article/details/82357239
普通quickSelect
普通的quickSort实现起来比较简单,每次固定选择最左侧或最右侧元素为pivot,设置low指针为splitPoint,splitPoint左侧的点都小于pivot,splitPoint及它右侧的点都大于等于pivot。
Lomuto partition scheme: https://en.wikipedia.org/wiki/Quicksort#Algorithm1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47import java.io.*;
import java.util.*;
public class Solution {
public static void main(String[] args) {
/* Enter your code here. Read input from STDIN. Print output to STDOUT. Your class should be named Solution. */
Scanner scanner = new Scanner(System.in);
int len = scanner.nextInt();
int[] input = new int[len];
for(int i = 0;i<=input.length-1;i++){
input[i] = scanner.nextInt();
}
quickSort(input, 0, input.length-1);
}
private static void quickSort(int[] input, int low, int high){
if(low>=high){
return;
}
int mid = partition(input, low, high);
quickSort(input, low, mid-1);
quickSort(input, mid+1, high);
}
private static int partition(int[] input, int low, int high){
int pivot = input[high];
int splitPoint = low;
for(int i = low; i<=high; i++){
if(input[i]<pivot){
swap(input, i , splitPoint);
splitPoint++;
}
}
swap(input, high, splitPoint);
for(int i = 0;i<=input.length-1;i++){
System.out.print(input[i]+" ");
}
System.out.println();
return splitPoint;
}
private static void swap(int[] input, int i, int j){
int num = input[i];
input[i] = input[j];
input[j] = num;
}
}双路quickSelect
思路是选择最左侧的点为pivot,然后设置两个pointer i和j,i一直运动直到遇到比pivot大的元素,j一直向左运动直到遇到比pivot小的元素,如果此时i<=j,那么swap(i,j)。那么最后j及j之前的都是小于pivot的,i及i之后的都是大于pivot的。
1 | class Solution { |
topK + 多个sorted array/sorted list
这种类型题本质上就是topK问题,最简单的想法当然是像topK一样把所有元素都加入到一个K大小的PQ中就好了,这样确实能得到结果,但是时间复杂度是O(nlogn),n是总共元素的个数。一个很重要的优化方式是我们应该注意到给我们的都是排好序的元素,所以我们要利用他们排好序的性质。思路类似于Merge K sorted LinkedList,在那道题中我们使用Priority Queue,并且利用了Sorted LinkedList的next指针去找到下一个元素,这类题目我们可以利用index去找到下一个元素,时间复杂度是O(klogk)
378. Kth Smallest Element in a Sorted Matrix:我们把sorted matrix看成是多个sorted array,我们先把所有sorted array的第一个元素加入PQ中,然后每次我们从PQ中取出一个元素以后,我们都把这个元素所在的sorted array的下一个元素加入到PQ中去(所以我们需要存储目前的index),可以发现和Merge K Sorted LinkedList非常相似。当然这里我们把横着或者竖着当成sorted array都可以。
1 | class Solution { |
- Find K Pairs with Smallest Sums:这道题本质上和上道题完全一样,但是需要变化一下,如下图,我们把所有他们的和求出来就会发现其实和上一道题完全一样了。
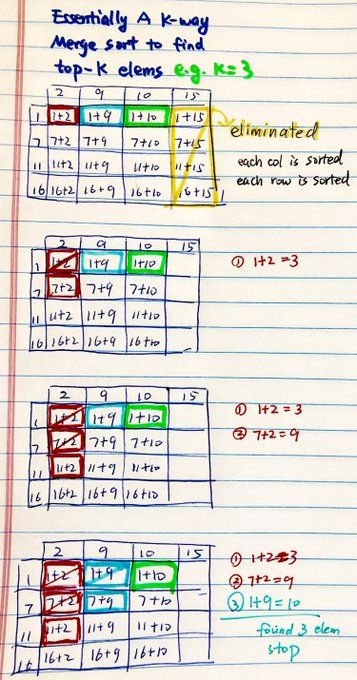
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
//int[] num; num[0]存num1,num[1]存num2,num[2]存num2的index
List<List<Integer>> ans = new LinkedList<>();
if(nums1.length==0 || nums2.length==0 || k==0) return ans;
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b)->{
return a[0]+a[1] - b[0]-b[1];
});
for(int i =0;i<=nums1.length-1&&i<=k-1;i++){
pq.offer(new int[]{nums1[i], nums2[0], 0});
}
while(k>0 && pq.size()!=0){
int[] tmp = pq.poll();
List<Integer> l = new LinkedList<>();
l.add(tmp[0]);
l.add(tmp[1]);
ans.add(l);
k--;
if(tmp[2]==nums2.length-1)
continue;
pq.offer(new int[]{tmp[0], nums2[tmp[2]+1], tmp[2]+1});
}
return ans;
}
}
处理流数据中的Top K问题:system design
使用一个hashmap加一个最小堆。HashaMap + PriorityQueue
每次进来的数据先在hashmap中加1。如果:
- 新进来的数据已经在堆中,调整堆(java的priority queue实现不了,但是这是系统设计题,调整操作在堆中是很简单的,因为只需要去判断一下改变的这个元素和它堆下面的元素的大小关系)
- 新进来的数据不再堆中
- Priority Queue的size小于K,新进来的数据放入最小堆中
- Priority Queue的size等于K,我们比较新进来数据在hashmap的value与最小堆在hashmap的value。如果大于,排除最小堆的最小值加入这个新的string,否则什么都不做。
1 | HashMap<String, Integer> map = new HashMap<>(); |